みなさん、こんにちは。長介です。連休だから、個人的にやりたかったことに時間が割けると思ったら大間違い。
この感じだと、一生時間に追われるのだろうと感じ始めました。
さて、少し前から気になっていた「系列問題」という知育課題について、この機会に考えてみました。皆さんは、この「系列」という言葉を聞いたことがありますか？
系列問題は、問題中にある法則を見つけ出し、問われている答えを導き出すものです。そのように、順番を予測したり、関係性をまとめたりと、脳が忙しくなる系列問題ですから、知育活動の観点からも有用なわけですね。
そして、この系列という規則性を幼児期に体感しておくことは、様々な波及効果を生むのでは、と少々飛躍気味にもとらえまして。
今回は、家庭で、法則を簡単に体感できる知育活動について考察してみました。
知育活動に情熱をもつ、みなさまの一助となれば幸いです。
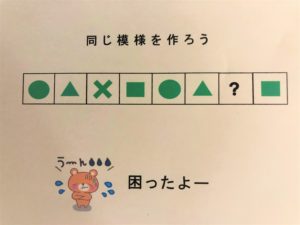
法則を理解するには、法則を作ろう
そもそも、この「系列」は、割と一般的な知育テーマといえるでしょう。幼児教室「めばえ教室」の教具にもありますし、お受験向け教室の「こぐま会」や、幼児教室「ピグマリオン」にも登場します。書店でチラ見した小学校受験向けのドリルのなかにもありました。
その系列問題は、法則の最小単位が「かたまり」ごとに並んでいて、「？」の部分を解答するといった問題です。そのため、その「かたまり」に分解できれば、答えは明快です。
法則を問う問題である系列問題。記号や図形が、一定の規則にそって並んでいます。
しかし、3歳になりたてのころなど、幼児期にその法則を促すことは、かなり困難といえるでしょう。2歳前半ごろから取り組んだ「めばえ教室」の系列問題も、いまひとつピンと来ていない様子でした。
かといって、更に説明が難しくなる「プリント」を使って理解を促すなど、到底無理と判断。そこで、まずは「系列問題はどのような問題なのか」という前提を、あらかじめ教えておくほうが良いと思いました。もちろん、言葉の意味を教えるのではなく、提示しているパズルのルールはどんなものか、というものです。
そのために、系列問題の「パターン」を使って、ブロックを使って「法則」を創る遊びを促してみました。
具体物を使って法則で遊ぶ！いわば「法則あそび」
うちの子供の場合は、この法則を使ったブロック遊びを、3歳半ごろに始めてみました。しかし、開始時期は、2歳後半ごろでも提示は可能でしょう。やってることの本質は、順番の認知と、ブロック並べですから。
なお、ここでは、ニキーチンの積み木と、自作のブロックを使ってご紹介しています。しかし、色付きのマグネットなどのほか、様々なもので代用ができるでしょう。
では、早速みてみましょう。
手順① まずは3つのブロックを並べ、ひとつの法則を作っておきます。
青・赤・黄のならびがひとつの法則となることを体感してもらいます
手順② そして、その3つのブロックを1組として、他の”かたまり（塊）をつくってもらいます。ここでは、全部で3つのかたまりを作ってもらっています。
手順③ 出来たかたまりを、他の塊とくっつけます。
※1つの「かたまり」が1つのルール（法則）ということを理解していれば、一番最初に提示してある「青・赤・黄」の並びに続けて、順番に並べてもらう方法も良いと思います。
手順④ そして、わけた塊が全部同じになるように、再度分解してもらいます。最小単位がくっついて並んでいることの理解を促します。
※大人には当たり前すぎてナンセンスな作業に見えることでしょう。ですが、私たちが解法を教えることなく、同じルール（法則）のものが繰り返されていることを体感してもらうのに必要な作業だと思います。実際に、この系列問題の仕組みを理解してからは、初めての系列問題での正答率が向上しました。
ここまでが、あくまで系列問題を活用した、「法則」の成り立ち理解を促すトレーニングです。この作業は、きっとお子さんもすぐに慣れるなれると思います。
次に、並びのひとつを空欄（？）にしたパターンカードを作成・提示してみましょう。
提示する系列パターンを作成し、提示してみましょう。
「この並びの中でどのような記号が入るのか」を質問する方法として、
①パターンカード化による提示
②ニキーチンの積み木ブロックそのものを並べ、途中に「？」を挿入
といった提示が考えられるでしょう。
では、どのような系列パターンを提示するのが良いでしょうか。
【例：レベル①】
6個のブロックを使い、2つ1組の法則を3組ならべましょう。
【例：レベル②】
9個のブロックを使い、3つ1組の法則を3組ならべましょう。
【例：レベル③】
8個のブロックを使い、4つ1組の法則を2組ならべましょう。
暫定的に、上記のようなレベル分けをしていますが、使用ブロック数と、空欄数の調整で、難易度が変化します。最初は簡単な問題から提案し、お子様の様子をみながら、徐々に難易度をあげてみましょう。
考えた上記のようなパターンに沿って、あらかじめブロックを並べておきます。そして、「？」の部分に何が入るのかを問います。
正解でも不正解でも、その答えがあっているかどうかを、最小単位に分解し、確認をしましょう。お子様自身が最小単位に分解できる場合は、お子様自身で、難しければ提示者が行いましょう。
その確認方法の声がけ例は、「1つの塊が、他の塊と同じになるように分けると～こうなるね。あれ、でもこの？の部分だけ違うな～」などなど。
「同じになるように”？”も一緒に動かしてね」※このあたりの理解が足りなそうであれば、上記「法則を分解したりくっつけたりして、法則の最小単位を知ろう」の①～④を繰り返してみてください。
「どの法則の繰り返しっぽいのかな」という推測でわけて、「そして”？”の部分に何を入れると、わけた部分がすべて同じになるのか」がわかるような声掛けをしてあげられれば理想的ですね。
さて、正解なら提示した問題は終了です。不正解なら怒ります（ダメ、ぜったい笑。）
感覚的にわかるようになるまで、何度でもやると良いと思います。問題の仕組みを理解して慣れてしまえば、初見で自然に解答できるようになると思います。
また、子供が記憶して解答するようになった気配とともに、お子さまの正答率があがったら、法則の最小単位を増やし、全体のブロック数も増やしてみましょう。
この手の問題は、やり方を覚えてしまえばどなたでもできるようになる問題だと思います。しかしながら、何かと何かの間に関連を見出す訓練を行うことで、法則に対する感覚が磨かれてくると良いな、と思うわけであります。
なお、本記事で登場した教材の作り方などは、下記にまとめております。ご興味ある方の参考となれば幸いです。
皆さまの、家庭での知育の一助となれば幸いです。
